模式识别数据降维及分类

模式识别实验报告

1. 实验概述

1.1. 实验目的

1. 理解并实现PCA、LDA两种降维算法
2. 理解并实现QDF、KNN分类器
3. 比较分析不同降维方法与分类器组合在MNIST手写数字数据集上的性能差异

1.2. 实验环境

环境项	配置说明
操作系统	Windows10
Python版本	3.11
主要依赖库	Numpy, Matplotlib, PyTorch（仅加载数据）
硬件配置	CPU：Intel i5, 内存：8GB

2. 算法实现

2.1. PCA

通过线性变换将原始数据投影到特征向量方向上，保留方差最大的几个成分（无监督降维）

1. 计算均值，数据中心化
2. 计算协方差矩阵
3. 特征值分解：求解协方差矩阵的特征值和特征向量
4. 选择主成分：按特征值大小降序排序，选择前k各特征向量作为投影方向
5. 数据投影：将原始数据投影到选定的主成分上

2.2. LDA

找到投影方向，使得同类样本尽可能接近，不同类样本尽可能远离（有监督降维）

1. 计算每个类别的均值向量和总体均值
2. 计算类内散度矩阵 $S_w$
3. 计算类间散度矩阵 $S_b$
4. 求解广义特征值问题，求解 $S_w^{-1} S_b$ 的特征值和特征向量
5. 按特征值降序排序，选择最大的k个特征值对应的特征向量作为投影方向

2.3. QDF

假设每个类别的数据服从高斯分布，通过估计每个类别的均值和协方差矩阵构建二次判别函数进行分类

1. 计算每个类别的先验概率
2. 计算每个类别的样本均值
3. 计算每个类别的样本协方差矩阵
4. RDA正则化解决模型过拟合问题
5. 选择判别函数最大的类别

2.4. KNN

找到样本距离最近的K个训练样本，采用投票机制，将样本分配给K个邻居中出现次数最多的那个类别

1. 遍历每个测试样本，计算其与所有训练样本的距离
2. 找距离最近的k个训练样本，并获取这k个邻居的标签
3. 统计这些标签出现次数，选择出现次数最多的标签

3. 实验步骤

3.1. 目录结构

├── mnist_data/             # 数据集
├── img/             		# 实验结果分析图
├── main.py                 # 主程序：实验配置、循环调度及结果汇总
├── pca.py                  # 降维算法：主成分分析（无监督）实现
├── lda.py                  # 降维算法：线性判别分析（有监督）实现
├── qdf.py                  # 分类器：带RDA正则化的二次判别函数
├── knn.py                  # 分类器：K近邻算法
├── data_loader.py          # 数据预处理：数据归一化及训练/验证/测试集的划分
├── plot_results.py			# 结果绘图处理
├── experiment_results.json	# 实验结果
├── experiment_results.txt	# 实验结果
└── requirements.txt		# 依赖库文件

3.2. 实验流程

3.2.1. 数据划分

利用 data_loader.py 对 MNIST 数据集进行预处理

• 加载与展平：将 $28 \times 28$ 的灰度图像展平为 $784$ 维特征向量，并进行归一化处理

• 数据集划分：将原始训练集按 9:1 随机划分为训练集（54,000张）和验证集（6,000张），保留独立的测试集(10,000张)

3.2.2. 特征降维

分别构建无监督的PCA特征子空间和有监督的LDA特征子空间

• PCA 子空间构建：遍历维度 $D \in {5, 9, 20, 50, 100}$，保留数据方差最大的前 $D$ 个主成分。

• LDA 子空间构建： $\text{LDA}$ 只在 $D \le K-1 $ 的维度上运行（$\text{MNIST}$ 有 $K=10$ 个类别，$\text{LDA}$ 最大降维维度为 $K-1=9$），当循环到 $D > 9$ 时，$\text{LDA}$ 实验自动跳过。

3.2.3. 分类器性能验证

在上述构建的每个子空间中，分别训练 QDF 和 KNN 分类器

• QDF 正则化验证：在每个维度下，遍历正则化参数 $\lambda$。验证当维度较高或样本分布不均时，引入 $\lambda$ 是否能通过平滑协方差矩阵来解决模型过拟合问题

• KNN 效率验证：记录 KNN 在不同维度下的测试时间。验证“维度灾难”对基于距离度量的懒惰学习算法计算效率的影响

4. 结果分析

4.1. 实验参数

变量	含义	实验值
dimensions	降维维度	PCA：[5, 9, 20, 50, 100] LDA：[5, 9] (受限于类别数 $K-1$)
knn_k_calues	KNN 邻居数 ($K$)	[1, 3, 5, 10]
qdf_reg_params	QDF正则化系数 ($\lambda$)	[0, 0.25, 0.5, 0.75, 1]

4.2. 结论分析

4.2.1. 同一子空间，同一分类器

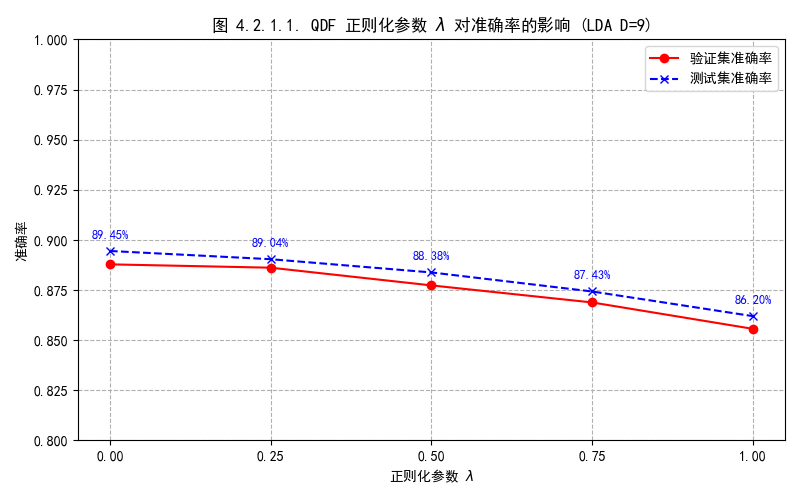
4.2.1.1. QDF正则化与模型稳定性分析

在 $LDA\ D=9$ 子空间中，正则参数从0到1，测试集准确率降低约3.25个百分点，在该子空间中非正则化的QDF表现最好，类别间的协方差矩阵没有出现明显的过拟合现象，说明已经足够稳定，正则化反而引入偏差，无需引入球面协方差来稳定模型

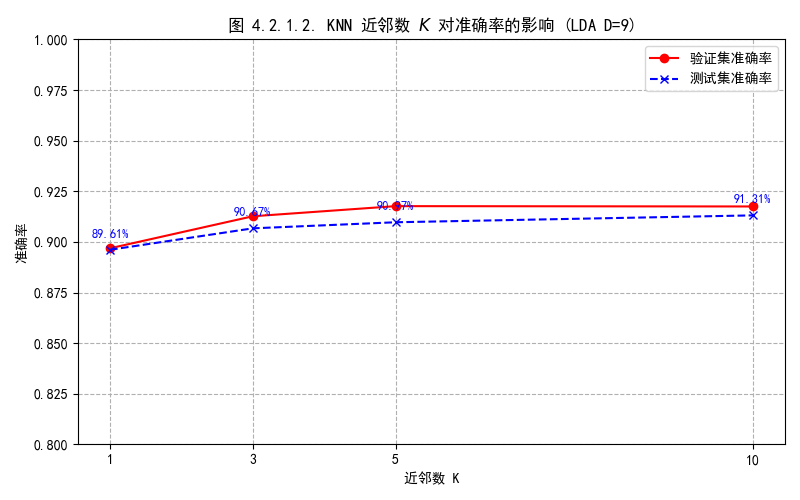
4.2.1.2. KNN的k值指定大小

在 $LDA\ D=9$ 子空间中，邻近数从1到10，测试集准确率有微弱上升，说明随着K值增大，模型抗噪能力更强，准确率提升并趋于稳定

4.2.2. 不同子空间，不同分类器

4.2.2.1. QDF与KNN分类器对比

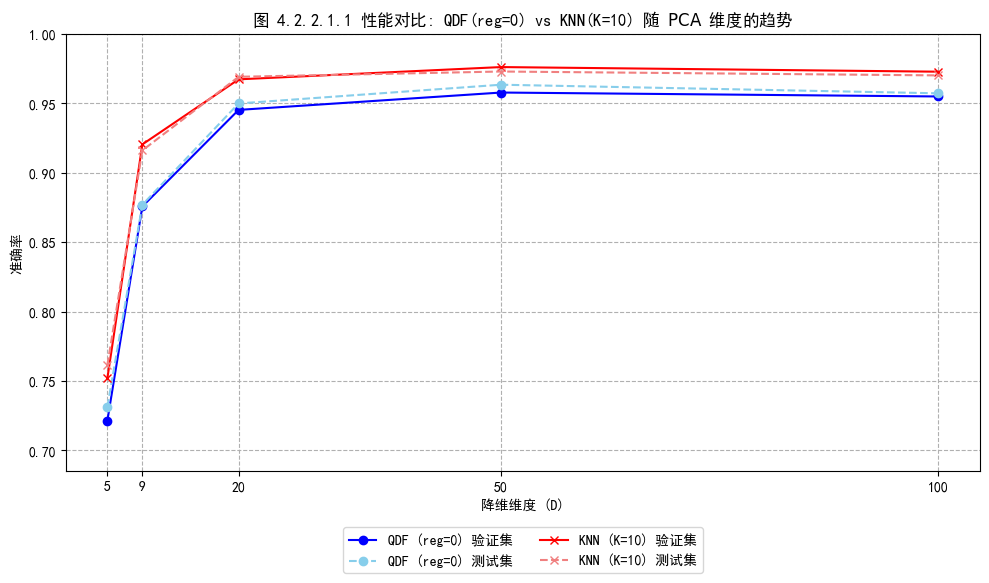
图 4.2.2.1.1 为两种分类器随 PCA 维度增加的准确率变化趋势对比图。整体上，随着降维维度增加，准确率有显著提高，并在 D≥50 后趋于平稳，可见对于 PCA 降维维度不能够过低，以充分保留数据集中重要信息。对比 KNN 与 QDF 分类器，在所有测试的维度上， KNN(K=10) 的性能始终优于 QDF(λ=0)，展现出更强的分类能力

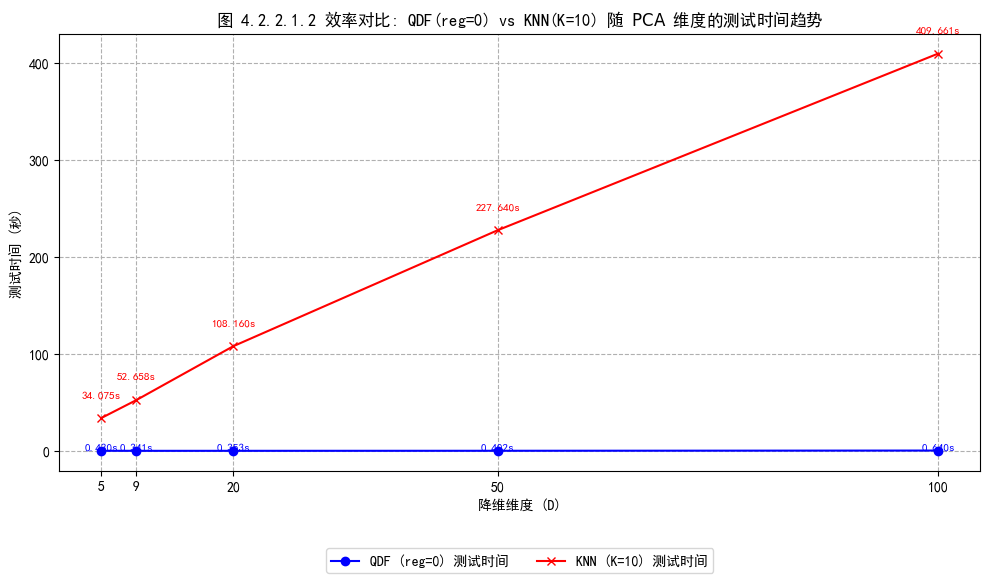
图 4.2.2.1.2 为两种分类器随 PCA 维度增加的测试时间变化趋势对比图。随着降维维度增加，QDF 的测试时间几乎不受影响，始终保持在1s以内，时间效率高；而 KNN 的测试时间随着维度的增加显著地线性增加，因为其每次预测都需要计算测试样本与所有训练样本在该维空间中的距离并排序，计算量高